REVISÃO

Locomoção humana sob a perspectiva dos sistemas dinâmicos: teoria e implicações clínicas

Human locomotion within dynamical systems perspective: theory and clinical implications

Kênia Kiefer Parreira de Menezes, D.Sc.*, Diego Leite, M.Sc.*, Patrick Roberto Avelino, Ft.**

*Programa de Pós-graduação em Ciências da Reabilitação, Escola de Educação Física, Fisioterapia e Terapia Ocupacional (EEFFTO), Universidade Federal de Minas Gerais, Belo Horizonte MG, **Universidade Federal de Minas Gerais, Belo Horizonte MG

Recebido em 15 de maio de 2019; aceito em 3 de julho de 2020.

Correspondência: Kênia Kiefer Parreiras de Menezes, Av. Pres. Antônio Carlos, 6627 Pampulha 31270-901 Belo Horizonte MG

Kênia Kiefer P. Menezes: keniakiefer@yahoo.com.br

Diego Leite: diego.xav@hotmail.com

Patrick Roberto Avelino: patrickpk4@yahoo.com.br

Resumo

A locomoção é uma função humana básica que permite ao indivíduo explorar seu ambiente e executar ações apropriadas. A locomoção também pode ser vista do ponto de vista energético, como uma forma de dissipar energia dentro de um sistema termodinâmico. Tradicionalmente, o controle da locomoção tem sido estudado sob a perspectiva de redes neuronais no sistema nervoso central. Abordagens mais recentes têm tentado fornecer uma visão diferenciada para o controle motor, como a abordagem dos Sistemas Dinâmicos ou Teoria dos Padrões Dinâmicos. Portanto, o objetivo do presente estudo foi revisar os princípios teóricos da aplicação da abordagem dos sistemas dinâmicos para o entendimento da locomoção humana e discutir as implicações práticas dessa abordagem para a área da reabilitação. A abordagem dos Sistemas Dinâmicos é uma teoria que assume a importância dos vários subsistemas do organismo humano, que seriam controlados pelas leis dinâmicas da física. De forma geral, seria um sistema de auto-organização que busca estratégias mais eficazes de acordo com os recursos disponíveis e as limitações impostas pelo ambiente. Através dessa linha de raciocínio, podemos interpretar como acontece o processo de locomoção humana, seus padrões de ocorrência e ainda aplicá-la para a marcha de populações especiais, como paralisia cerebral, acidente vascular encefálico, dor lombar, dentre outros.

Palavras-chave: locomoção, teoria de sistemas.

Abstract

Locomotion is a basic human function, which allows the individual to explore his environment and perform appropriate actions. The locomotion also can be seen from the energy point of view, as a means of dissipating energy in a thermodynamic system. Traditionally, the locomotion control has been studied from the standpoint of neural networks in the central nervous system. More recent approaches have been tried to provide a different perspective for motor control, such as the approach of Dynamical Systems or Dynamical Patterns Theory. Therefore, the objective of this study was to review the theoretical principles of the application of dynamical systems approach to understanding human locomotion and discuss the practical implications of this approach to the field of rehabilitation. The approach of Dynamical Systems is a theory that assess the importance of the various subsystems of the human body, which would be controlled by the dynamic laws of physics. In general, would be a system of self-organization looking for the most effective strategies in accordance with available resources and constraints imposed by the environment. Then, we can interpret the process of human locomotion, their patterns of occurrence and apply it to the gait of special populations, such as cerebral palsy, stroke, low back pain, among others.

Keywords: locomotion, systems theory.

Introdução

A locomoção é uma função humana básica, que permite ao indivíduo explorar seu ambiente e executar ações apropriadas [1,2]. A locomoção também pode ser vista do ponto de vista energético, como uma forma de dissipar energia dentro de um sistema termodinâmico [2]. Tradicionalmente, o controle da locomoção tem sido estudado sob a perspectiva de redes neuronais no sistema nervoso central (SNC) [3-8]. É assumido que existem redes especializadas na medula espinhal que seriam responsáveis pelo padrão rítmico da locomoção, denominadas Geradores de Padrão Central [3,5,8]. Sob essa perspectiva, sinais vindos de níveis superiores do SNC (exemplo, córtex cerebral, centro mesencefálico da locomoção) seriam responsáveis por ativar esses geradores de padrão, que por sua vez, desencadeariam o padrão oscilatório de flexão em um membro e extensão no membro oposto observado nas formas de locomoção como a marcha e a corrida [3,8]. Informações aferentes vindas de receptores musculares, receptores articulares do quadril e mecanoceptores na planta dos pés seriam importantes para moldar o padrão de locomoção, tornando-o adaptativo a condições externas [7].

As evidências científicas que sugerem a existência desses geradores de padrão para a locomoção são baseadas em estudos em animais. Experimentos em gatos tentaram comprovar a existência dessas redes neuronais por meio de diferentes condições experimentais como, descerebração, transecção medular e bloqueio de informação aferente [9-11]. Esses estudos evidenciaram que mesmo sem informação aferente ou retirando-se a comunicação com centros superiores do SNC, o padrão típico de locomoção podia ser licitado quando esses animais eram postos em uma esteira e tinham o seu peso corporal sustentado, esse tipo de marcha foi denominado marcha fictícia. Estudos tentaram estabelecer a existência desses geradores de padrão em humanos por meio de experimentos em indivíduos com lesão medular [12,13] e da análise de padrões temporais e eletromiográficos da marcha [5]. Esses estudos são limitados para o entendimento da locomoção, pois assumem uma relação de causa e efeito entre lesões induzidas no SNC e fenômenos neurofisiológicos e o controle da locomoção. Dessa forma, essa perspectiva teórica para o entendimento da locomoção não leva em conta, de maneira apropriada, os problemas levantados por Bernstein, como a variabilidade dependente do contexto [14].

Abordagens mais recentes têm tentado fornecer uma visão diferenciada para o controle motor, como a abordagem dos Sistemas Dinâmicos ou Teoria dos Padrões Dinâmicos [15-17]. Essa abordagem teórica é baseada nos princípios da sinergética, uma teoria física que assume que a estrutura ou mudanças de estrutura em sistemas abertos e em não equilíbrio ocorrem de maneira auto-organizante. As transições de fase ocorrem quando condições ambientais (ou parâmetros de controle) atingem um ponto crítico. Esses sistemas são governados por poucos graus de liberdade, entretanto, podem exibir comportamentos altamente complexos [15]. As predições dessa nova abordagem foram obtidas por meio de estudos que analisaram movimentos rítmicos dos dedos ou mãos de acordo com um parâmetro de controle (frequência de oscilação dos segmentos) que exerceu influência sobre o parâmetro de ordem (padrão de fase entre os segmentos de cada membro) [16]. Aumentando-se a frequência de oscilação foi observada uma transição de fase (bifurcação) de um padrão fora de fase para um padrão em fase, transição ocorrida de maneia auto-organizante, sem necessidade de evocação de um processo cognitivo ou representacional. Partindo-se do pressuposto de que a locomoção é um processo rítmico, as predições dessa nova abordagem têm sido utilizadas para o seu entendimento, de forma a realizar uma descrição dinâmica e predições de seus parâmetros [2,18,19].

Considerando-se o contexto da reabilitação física, meios de locomoção (marcha, corrida) são utilizados como desfechos clínicos [20,21], marcadores do estado funcional [22] e formas de intervenção [23-25]. Dessa forma, a locomoção é um ponto chave dentro da área da reabilitação. Quando analisados os estudos sobre locomoção na área da reabilitação, é possível perceber que grande parte tem como referencial teórico, de forma explícita ou implícita, as abordagens mais tradicionais de controle motor. Entretanto, estudos recentes na área da reabilitação têm utilizado como referencial teórico a abordagem dos sistemas dinâmicos [19], Hamill et al. [26] e Ho et al. [27], como exemplos. É possível que esses estudos forneçam importantes subsídios para a prática clínica em fisioterapia e possam servir como embasamento teórico para algumas intervenções já utilizadas. Além disso, é possível que novas intervenções, pautadas na abordagem dos sistemas dinâmicos, possam surgir.

Portanto, os objetivos deste ensaio teórico foram: 1) Revisar os princípios teóricos da aplicação da abordagem dos sistemas dinâmicos para o entendimento da locomoção humana e 2) discutir as implicações práticas dessa abordagem para a área da reabilitação.

Material e métodos

Para condução do presente estudo foram pesquisados estudos nas bases de dados Medline e Science Direct. Os descritores utilizados para a busca bibliográfica, de acordo com o MeSH, foram: Locomotion, Nonlinear Dynamics, Systems Theory, Coordination e Walking. Além disso, foram pesquisados artigos e capítulos de livros de autores renomados na área, como Kenneth G. Holt. A partir da leitura dos títulos e resumos de todo o material encontrado, foram selecionados os estudos e capítulos de livros mais pertinentes para a condução deste ensaio teórico. Os principais achados desses estudos, bem como suas implicações para o entendimento da locomoção humana e para a área da reabilitação, são discutidos a seguir.

Resultados e discussão

Modelos teóricos para a locomoção - Oscilador harmônico híbrido e Escapement driven damped inverted pendulum/ mass-spring system

Como ressaltado anteriormente, a abordagem dos sistemas dinâmicos tem como princípio o estudo do controle e coordenação dos movimentos humanos considerando sistemas oscilatórios, rítmicos. Esses sistemas seguem uma dinâmica não linear e são governados por leis naturais (leis físicas). Dado que esses sistemas são governados por leis físicas, é possível realizar predições de seus parâmetros por meio de equações matemáticas [28]. A seguir serão discutidos alguns modelos teóricos, que por meio de equações matemáticas, são capazes de explicar a locomoção humana. O primeiro desses modelos é o Oscilador Harmônico Híbrido.

Analisando a fase de balanço da marcha humana, o membro inferior oscila como um todo, sendo a articulação do quadril o eixo de rotação. Além do componente gravitacional, que seria a massa e comprimento dos segmentos dos membros inferiores e a ação da gravidade sobre eles, existe um componente elástico, representado pelos músculos, tendões, fáscias e ligamentos presentes em todo o membro inferior, todos esses subcomponentes são representados por uma mola que representa a rigidez global do sistema. Considerando que esse sistema oscilatório possui dois componentes, um gravitacional e outro elástico, ele é considerado um sistema híbrido. Além disso, é um sistema harmônico porque conserva energia durante sua oscilação [18,19]. A equação Newtoniana que representa esse modelo é apresentada na Equação 1. Onde, ϕ é o deslocamento angular do pêndulo (ou do quadril), sua segunda derivada (ϕ) é a aceleração angular, m a massa da perna, Le o comprimento equivalente do eixo de rotação até o centro de massa da perna e kb² representa a rigidez dos tecidos. Considerando-se que a amplitude de oscilação é pequena (ϕ < 20°), podemos assumir que sinϕ ≈ ϕ e cosϕ ≈ 1. Logo, a equação pode ser simplificada de acordo com a Equação 2. Essa equação contêm os dois componentes do modelo, o momento de força pela gravidade e o momento de força pelo componente elástico. Nesse modelo, o damping (mecanismos de perda de energia) e o forcing (mecanismos de injeção de energia no sistema) não são considerados para a determinação da frequência de oscilação do pêndulo (embora eles influenciem na amplitude de oscilação).

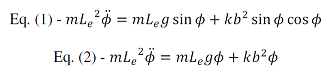
A partir dessa equação é possível obter equações para predição da frequência preferida de locomoção e para a rigidez da perna durante diferentes formas de locomoção (ver Obusek et al. [29] e Holt et al. [18] para mais detalhes). O segundo modelo para o entendimento da locomoção humana considera os componentes damping e forcing citados anteriormente. Esse modelo é utilizado para a fase de apoio da marcha, na qual o membro inferior é modelado como um pêndulo invertido, pois o eixo encontra-se agora na articulação do tornozelo [2,19,28,30]. Nesse modelo, o momento devido ao damping corresponderia às perdas de energia por fricção tecidual e pelo contato inicial do membro oposto (que estava na fase de balanço) e para manter a oscilação do pêndulo (já que ocorrem perdas de energia) temos o componente forcing, que corresponderia aos inputs de energia no sistema, como a força aplicada durante a fase de push-off da marcha [2,19]. O instante para fornecimento de energia é determinado pela própria dinâmica do sistema, dispensando a presença de processos probabilísticos. A equação desse modelo é apresentada na Equação 3. Sendo que, FL cos θ seria o componente forcing (injeção de energia no sistema), mLg sin θ o componente gravitacional, kb sin θb cos θ o componente elástico e c(θ)b cos θ o componente damping (perdas de energia por fricção e pelo contato inicial contralateral).

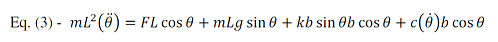
Potencialmente, esse modelo pode ser utilizado para estimar as diferentes fontes de energia para a locomoção. Também é possível realizar predição da rigidez do membro, partindo-se do pressuposto que o oscilador está em equilíbrio, ou seja, o componente forcing é igual ao componente damping.

Desenvolvimento da locomoção sob a perspectiva dos Sistemas Dinâmicos

Um estudo de Holt et al. [31] investigou como crianças na fase de aquisição de marcha descobrem a dinâmica do sistema pêndulo / mola para a locomoção. Para tanto, esse autor investigou a cinemática e cinética da marcha de crianças no momento da aquisição de marcha e durante os sete meses subsequentes, realizando reavaliações mensais. Foi observado que, entre o momento de aquisição da marcha e um mês após, ocorreu um aumento no comprimento do passo e na frequência do passo (sem alterações antropométricas concomitantes). Outro resultado foi que o pico de força de escapamento (peak escapement force) foi negativo, o que indica que ele ocorreu após o contato inicial do pé, ou seja, durante o apoio duplo, momento no qual teria um efeito mais adaptativo, um efeito de propulsão. Já a aceleração angular do centro de massa tornou-se mais positiva no momento do apoio duplo, indicando que ela ocorreu na mesma direção da linha de progressão. Uma característica básica do mecanismo pendular de marcha é a restrição dos movimentos no plano sagital, tanto na fase de apoio, quanto de balanço, com poucos movimentos nos planos transverso e frontal. Foi observado que as crianças após um mês da aquisição da marcha apresentaram um aumento nos movimentos da perna no plano sagital. Entretanto, sem alterações nos planos frontal ou transverso.

Além de mecanismos passivos (elasticidade dos tecidos biológicos) e gravitacionais (massa dos segmentos sob a ação da força da gravidade), forças musculares podem exercer influência sobre essa dinâmica, podendo restringir ou facilitar. Dessa forma, crianças no período após aquisição da marcha aprendem a prover forças que podem complementar a dinâmica do sistema pêndulo / mola, permitindo assim, uma máxima progressão para frente do centro de massa com um custo muscular (energético) mínimo [31].

O aprendizado de uma nova dinâmica pode ocorrer de maneira abstrata. Modos de locomoção que sejam mecanicamente e metabolicamente eficientes e estáveis são descobertos por um processo de experimentação. Esse modo de locomoção pode ser de alguma forma, “sentido” pelo sistema neurofisiológico e utilizado para fortalecer conexões neurais que produzem o escapamento (escapement) apropriado. Futuros estudos deverão investigar em detalhes como se dá esse processo de descoberta e aprendizado de uma nova dinâmica [31].

De acordo com Holt et al. [32] o desenvolvimento da dinâmica da locomoção envolve duas fases. A primeira foi citada anteriormente. A segunda fase ocorreria nos próximos meses e corresponderia ao desenvolvimento de uma relação de 1:1 entre a rigidez (que determina a frequência de oscilação) do componente elástico e o componente pendular (dependente das propriedades antropométricas e da ação da gravidade). Para Holt et al. [32] essa relação seria necessária para que os dois componentes oscilatórios ajam em ressonância, tornando possível realizar predições de seus parâmetros (e.g. frequência preferida). Entretanto, esses autores ressaltam que nem sempre essa relação é mantida numa relação de 1:1, como podemos perceber na corrida de adultos e na locomoção de crianças com Paralisa Cerebral (PC), meios de locomoção nos quais o componente elástico exerce maior influência, seja por meio de contração muscular (no caso da corrida) ou por meio de propriedades musculares passivas (no caso de crianças com PC).

Holt et al. [32] demonstraram nesse estudo que durante os sete meses após a aquisição da marcha as crianças apresentam um aumento no componente elástico do modelo (>n), o que faz com que a relação se torne > 1:1 (valores de n chegam a aproximadamente 3 à partir do terceiro mês de marcha), exceto no primeiro mês quando essa relação é próxima de 1:1. A hipótese levantada por esses autores é a de que nessa idade, as crianças ainda estão adquirindo aprendizado sobre como utilizar menos o mecanismo elástico do modelo e mais o mecanismo pendular, de acordo com as massas e comprimentos dos segmentos dos membros inferiores que vão se modificando de acordo com o desenvolvimento. É assumido que apenas a partir dos três anos de idade as crianças seriam capazes de refinar a dinâmica da locomoção, de forma a escalonar a relação entre o componente elástico e o pendular (formando uma relação de 1:1), reduzindo assim, o gasto energético para a locomoção e aumentando a estabilidade. Um achado interessante é o de que a relação é próxima de 1:1 logo após a aquisição da marcha, mas vai se distanciando desse valor ideal durante os sete meses subsequentes. A interpretação de Holt et al. para esse fenômeno é de que no início, a constraint para a locomoção é apenas a estabilidade para realizar a tarefa desejada no ambiente, sendo que os deslocamentos são curtos (e.g. alcançar a mãe ou um brinquedo próximos), somente após algum tempo, o gasto energético passa a ser uma constraint para a locomoção, momento no qual surge a necessidade de maiores deslocamentos no ambiente.

Esses estudos fornecem uma visão alternativa para a compreensão do desenvolvimento da locomoção, visto tradicionalmente como um processo dependente da neuromaturação do SNC [33]. Futuros estudos poderão investigar o desenvolvimento da locomoção, sob a perspectiva da abordagem dos sistemas dinâmicos, acompanhando crianças até a idade de três anos, momento o qual, aparentemente, as crianças adquirem um padrão mais maduro de locomoção, explorando uma relação de 1:1 entre os componentes elástico e pendular do modelo.

Padrões de coordenação durante a locomoção

Os estudos sobre coordenação intersegmentar, iniciados pelos experimentos que investigaram a coordenação entre dedos ou mãos [16,34] foram expandidos para a análise de padrões de coordenação entre diferentes segmentos durante a locomoção [35-37]. Esses estudos partem do pressuposto de que diferentes segmentos podem funcionar como pêndulos que oscilam em ressonância durante a locomoção.

Já foi demonstrado que em velocidades baixas de marcha (abaixo de 3,8 km/h) o padrão de coordenação entre pelve e tronco (tórax) segue em um padrão em fase, ou seja, os dois segmentos movimentam-se, aproximadamente, na mesma direção. Entretanto, quando a velocidade de marcha é experimentalmente aumentada para valores acima de 3,8 km/h, ocorre uma transição (bifurcação) de um padrão mais em fase para um padrão fora de fase [36,37]. Nesse exemplo, a relação de fase entre os segmentos (pelve e tronco) seria o parâmetro de ordem e a velocidade de marcha corresponderia ao parâmetro de controle. É observado que antes da transição ocorre um aumento na instabilidade do padrão que é operacionalizado pelo desvio-padrão da fase relativa entre pelve e tronco. Dentro da abordagem dos sistemas dinâmicos é sabido que transições de fase ocorrem na presença de uma perda na estabilidade do padrão, sendo que um novo padrão estável é alcançado após a transição (multiestabilidade). Essa transição de fase seria importante para alcançar um aumento no comprimento do passo, condizente com aumentos na velocidade de marcha, mas mantendo-se o tronco, e consequentemente, a cabeça, orientada para frente, na direção em que o indivíduo se locomove.

Outro padrão de coordenação já investigado na locomoção humana seria a coordenação entre membro inferior e membro superior contralateral [35]. Em velocidades baixas de marcha (abaixo de 2,7 km/h) o padrão de coordenação entre o membro superior e o membro inferior está numa relação de 2:1, ou seja, os braços realizam duas fases de balanço por passo, já em velocidades maiores, a razão é de 1:1, ou seja, é realizada uma fase de balanço do braço para cada passo. Alterações nesses padrões de coordenação (tronco x pelve; membro superior x inferior) já foram demonstradas em indivíduos com disfunções ortopédicas ou neurológicas, como hemiplégicos e indivíduos com dor lombar [38-41] e serão discutidas posteriormente neste texto.

Tipos de locomoção – marcha x corrida

A locomoção humana exibe duas formas básicas, que podem ser observadas de acordo com a velocidade do deslocamento [42]. Esses dois mecanismos básicos seriam: o mecanismo rígido de marcha, similar a um “pêndulo invertido”, e o mecanismo flexível de corrida, trote e salto, similar a uma "bola quicando" [43]. A marcha e a corrida são alvos de muitas pesquisas que buscam aplicar modelos biomecânicos na tentativa de compreender a dinâmica envolvida nessas atividades [44]. Esses dois tipos de locomoção têm componentes tanto de mola quanto de pêndulo, podendo assim o modelo híbrido ser usado para descrever ambos [2].

De acordo com os tipos de locomoção, podemos diferenciá-las pela contribuição relativa do componente elástico para a conservação de energia. Na marcha, observa-se o modelo do pêndulo, em que as trocas de energia potencial e energia cinética no centro de massa são alcançadas por meio dos efeitos gravitacionais [2]. Já a corrida é comparada a uma “bola quicando”, a maior parte da energia é conservada por armazenamento nas propriedades da mola, como os músculos e tecidos moles [2,42]. Adotando o modelo híbrido como referência, uma vez que a rigidez dos tecidos é maior durante a corrida, uma razão maior entre kb²: mLeg (constante n) seria encontrada [2]. Um estudo de Cavagna et al. [43], suporta a ideia de que a corrida pode ser descrita como uma sucessão de saltos verticais do corpo. O complexo sistema de músculos que se contraem e os tendões das pernas e pés representam a rigidez de uma mola vertical hipotética, sobre a qual todo o corpo salta a cada passo.

A transição entre esses dois tipos de locomoção comporta-se como uma transição de fase entre dois atratores, além disso ocorre de forma a minimizar o gasto energético do sistema musculoesquelético e cardiovascular [44,45]. Em velocidades acima de 8,0 km/h a corrida requer menor gasto energético (por metro percorrido) do que a marcha e a transição entre marcha e corrida ocorre próximo de uma velocidade de 8,0 km/h [45]. Diedrich et al. [45] investigaram em detalhes a transição entre esses tipos de locomoção e demonstraram que as mudanças em relação ao comprimento do passo e frequência de oscilação foram bastante modestas o que sugere que a transição entre os dois tipos de locomoção dependa mais do gasto energético.

Locomoção em populações especiais

A locomoção é, para os animais e seres humanos, uma função crítica que permitir a exploração do ambiente em busca de alimento, abrigo e um companheiro. Restrições funcionais nessa atividade podem advir de diversos fatores, sendo eles a fadiga, instabilidades (que podem levar a quedas ou medo de cair), força muscular limitada, dor e/ou controle neurológico insuficiente ou inadequado [2]. As mudanças qualitativas na coordenação do movimento emergem espontaneamente como resultado de inespecíficas e contínuas alterações nos parâmetros de controle [35]. Diversas são as patologias que podem comprometer a locomoção em humanos, como Paralisia Cerebral (PC), hemiplegia/ hemiparesia decorrente de Acidente Vascular Encefálico (AVE), dor lombar, uso de próteses nas pernas, doença de Parkinson, entre outros. No entanto, as disfunções de movimento não são apenas uma consequência de alterações estruturais, mas também podem ser entendidos como uma organização espaço-temporal anormal na coordenação do movimento [35].

A PC leva muitas vezes a déficits de força muscular e hipertonia [40]. Durante a marcha desses indivíduos, há um aumento na cocontração muscular, além de um aumento da rigidez muscular passiva que aumentam a rigidez global dos membros. Segundo o modelo híbrido, é possível calcular o valor da constante n se o sistema está em sua frequência natural e este valor irá indexar a rigidez do membro em relação ao componente gravitacional [2]. Em crianças com hemiplegia espástica, o valor médio de n é 2,43, valor significativamente diferente das crianças com desenvolvimento típico, onde n=2 [46]. Esses resultados indicam que existe um aumento da rigidez em indivíduos com PC, que provoca um aumento da frequência de locomoção. Esse aumento de rigidez associado a outros padrões cinemáticos que a marcha de crianças com PC apresenta, suportam a ideia de uma associação desse tipo de locomoção com a corrida. A estratégia seria aproveitar-se mais das propriedades elásticas da corrida, o que não pode ser alcançado na marcha tradicional [2]. Esse padrão, contudo, apresenta custos energéticos mais elevados, uma vez que há um aumento no deslocamento vertical do centro de massa, além da presença de cocontração muscular excessiva [47]. Assim, os padrões da marcha de crianças espásticas podem não ser o típico, mas são muitas vezes funcionais, pois atingem o objetivo de locomoção através da utilização dos recursos disponíveis [46].

O AVE está associado muitas vezes a um comprometimento da capacidade de locomoção desses indivíduos, sendo divergente a literatura quanto à possibilidade ou não dessa coordenação ser mantida após esse episódio [39]. Indivíduos com hemiparesia devido a um AVE apresentam comprometimento sensório-motor múltiplo, que resultam em incoordenação do movimento [38]. No entanto, poucos estudos atualmente têm comparado diretamente os padrões de coordenação durante a locomoção de pacientes com AVE em relação a indivíduos saudáveis, de acordo com as ferramentas da abordagem dos sistemas dinâmicos. Stephenson et al. [39], ao colocar indivíduos pós-AVE e saudáveis em uma esteira e analisar os movimentos dos braços, não observou diferenças nas medidas de coordenação intersegmentar entre as populações, o que indica que a coordenação entre os movimentos do braço e da perna durante a marcha continua preservada nesses indivíduos.

Além disso, existiam nessas esteiras alças auxiliares que deslizavam em barras paralelas, caso o indivíduo as necessitasse para a atividade, e foi encontrado que os padrões de coordenação também não foram afetados pela utilização desses corrimãos de deslizamento. Já Lamontagne et al. [38] investigaram a coordenação e a estabilização dos segmentos axiais durante a marcha com e sem movimentos horizontais voluntários da cabeça, em indivíduos saudáveis e hemiparéticos por AVE. Os resultados desse estudo sugerem que as rotações de cabeça durante a caminhada modificam a coordenação do segmento axial em uma direção específica, enquanto as rotações pélvicas associadas com locomoção permanecem inalteradas.

A dor lombar é muitas vezes acompanhada por déficits no movimento. No entanto, não se sabe muito sobre como o movimento é afetado por esta condição e sobre seu impacto nas atividades funcionais [41]. Ao se comparar a marcha de indivíduos saudáveis com aqueles com queixa de dor lombar, encontrou-se um padrão de movimento mais rígido, menos flexível na coordenação pelve-tronco e ausência de diferenças significativas na cinemática dos componentes rotacionais [41]. Esses indivíduos não são capazes de realizar a transição entre um padrão em fase para um padrão fora de fase entre os segmentos pelve e tronco. Alguns autores justificam que seria um padrão protetor em resposta à dor, entretanto, estudos recentes já descartaram essa hipótese [48] e pouco se sabe sobre os fatores causais dessa alteração na coordenação intersegmentar.

Implicações para a reabilitação

Baseados na visão da abordagem dos sistemas dinâmicos sobre a locomoção humana, as consequências para a reabilitação devem ser consideradas. A reabilitação pode ser orientada para aproveitar ao máximo das adaptações teciduais emergentes (recursos dinâmicos disponíveis) [2].

Em uma marcha “anormal”, a reabilitação deve ser dirigida para a causa da anormalidade. Se um indivíduo apresenta uma alteração em seu padrão de marcha devido a uma diminuição da capacidade dos músculos para produzir força suficiente, ou por alterações na rigidez tecidual passiva, o tratamento deve ser focado nesse achado, e não na baixa velocidade, alta frequência, comprimento do passo curto e baixa amplitude de movimento, como exemplos. No entanto, se nada pode ser feito sobre a causa, ou esta não pode ser identificada, este padrão alterado deve ser aceito como o ideal para o indivíduo e o objetivo da reabilitação pode ser o de promover os recursos que possam maximizar esse padrão [2]. Estudos demonstram que indivíduos com deficiência que apresentam alterações nos recursos dinâmicos (ex. rigidez passiva, força muscular) exploram e desenvolvem os recursos remanescentes em seus padrões de marcha adaptados e, assim, intervenções clínicas destinadas a normalizar um padrão de marcha podem ser contraindicadas [19]. No entanto, deve-se, se for possível, por meio de uma intervenção, melhorar um recurso que esteja limitado, proporcionando assim, a emergência de um padrão de marcha considerado típico, que seja energeticamente mais eficiente, estável e, talvez, esteticamente melhor [27].

Conclusão

Como visto, a perspectiva teórica dos sistemas dinâmicos traz modelos e conceitos novos que nos permitem aplicar à locomoção humana e ao contexto da reabilitação. É uma teoria que assume a importância dos vários subsistemas do organismo humano, que seriam controlados pelas leis dinâmicas da física. De forma geral, seria um sistema de auto-organização que busca estratégias mais eficazes de acordo com os recursos disponíveis e as limitações impostas pelo ambiente. Essa proposta de abordagem, ao contrário da visão tradicional de controle motor, exclui a necessidade do controle do movimento por centros superiores do sistema nervoso. O modelo de oscilador harmônico híbrido, por exemplo, compara os membros inferiores a um pêndulo acoplado a uma mola e, dessa forma, o movimento ocorre tão somente através das propriedades elásticas e gravitacionais do sistema.

Através dessa linha de raciocínio, podemos interpretar como acontece o processo de locomoção humana, seus padrões de ocorrência e ainda aplicá-la para a marcha de populações especiais, como PC, AVE, dor lombar, dentre outros. Essas patologias estão associadas com alterações nas propriedades dos tecidos do sistema, o que leva à emergência de um novo padrão, a partir dos novos recursos disponíveis. Essa interpretação irá influenciar também a prática do terapeuta na reabilitação, que deve focar sua intervenção sobre os achados do sistema que possam proporcionar a emergência de um novo padrão (ex. fraqueza muscular, rigidez passiva) e não nas características da tarefa emergente (ex. velocidade, equilíbrio). Futuros estudos deverão investigar em mais detalhes as repercussões do uso desse referencial teórico no processo de reabilitação de diferentes populações clínicas.

Referências

1. Warren Junior W. Visually controlled locomotion: 40 years later. Ecological Psychology 1998;10:177-219. https://doi.org/10.1207/s15326969eco103&4_3
2. Holt K, Obusek J, Fonseca S. Constraints on disordered locomotion: A dynamical systems perspective on spastic cerebral palsy. Hum Mov Sci 1996;15:177-202. https://doi.org/10.1016/0167-9457(95)00043-7
3. Dietz V. Spinal cord pattern generators for locomotion. Clin Neurophysiol 2003;114:1379-89. https://doi.org/10.1016/s1388-2457(03)00120-2
4. Clarac F. Some historical reflections on the neural control of locomotion. Brain Res Rev 2008;57:13-21. https://doi.org/10.1016/j.brainresrev.2007.07.015
5. Ivanenko Y, Poppele R, Lacquaniti F. Motor control programs and walking. Neuroscientist 2006;12:339-48. https://doi.org/10.1177/1073858406287987
6. Knikou M. Neural control of locomotion and training-induced plasticity after spinal and cerebral lesions. Clin Neurophysiol 2010;121:1655-8. https://doi.org/10.1016/j.clinph.2010.01.039
7. van de Crommert H, Mulder T, Duysens J. Neural control of locomotion: sensory control of the central pattern generator and its relation to treadmill training. Gait Posture 1998;7:251-63. https://doi.org/10.1016/s0966-6362(98)00010-1
8. Duysens J, van de Crommert H. Neural control of locomotion; Part 1: The central pattern generator from cats to humans. Gait Posture 1998;7:131-41. https://doi.org/10.1016/s0966-6362(97)00042-8
9. Brown T. The intrinsic factors in the act of progression in the mammal. Proc R Soc Lond 1911;84:308-19. https://doi.org/10.1098/rspb.1911.0077
10. Grillner S, Zangger P. The effect of dorsal root transection on the efferent motor pattern in the cat's hindlimb during locomotion. Acta Physiol Scand 1984;120:393-405. https://doi.org/10.1111/j.1748-1716.1984.tb07400.x
11. Shik M, Orlovsky G, Severin F. Locomotion of the mesencephalic cat elicited by stimulation of the pyramids. Biophysics 1968;13:143-52.
12. Bussel B, Roby-Brami A, Rémi NO, Yakovleff A. Evidence for a spinal stepping generator in man. Paraplegia 1996;34:91-92.
13. Bussel B, Roby-Brami A, Azouvi A, Biraben A, Yakovleff A, Held J. Myoclonus in a patient with a spinal cord transection. Possible involvement of the spinal stepping generator. Brain 1988;111:1235-45. https://doi.org/ 10.1093/brain/111.5.1235
14. Turvey M, Fitch H, Tuller B. The Bernstein perspective I: The problems of degrees of freedom and context-conditioned variability. In: Hilssdale N, ed. Human motor behavior: An introduction. 1ª ed. New Jersey: Lawrence Erlbaum; 1982. p. 239-52.
15. Kelso J, Schöner G. Self-organization of coordinative movement patterns. Hum Mov Sci 1988;7:27-46. https://doi.org/10.1016/0167-9457(88)90003-6
16. Kelso J, Holt K, Rubin P, Kugler P. Patterns of human interlimb coordination emerge from the properties of non-linear, limit cycle oscillatory processes: Theory and data. J Mot Behav 1981;13:226-61.
17. Scholz J. Dynamic Pattern Theory - Some implications for therapeutics. Phys Ther 1990;70:827-43. https://doi.org/10.1093/ptj/70.12.827
18. Holt, K, Hamill J, Andres R. The force-driven harmonic oscillator as a model for human locomotion. Hum Mov Sci 1990;9:55-68. https://doi.org/10.1016/0167-9457(90)90035-C
19. Fonseca S, Holt K, Saltzman E, Fetters L. A dynamical model of locomotion in spastic hemiplegic cerebral palsy: Influence of walking speed. Clin Biomech (Bristol, Avon) 2001;16:793-805. https://doi.org/10.1016/s0268-0033(01)00067-5
20. Lee M, Kilbreath S, Singh M, Zeman B, Lord S, Raymond J, Davis G. Comparison of effect of aerobic cycle training and progressive resistance training on walking ability after stroke: a randomized sham exercise-controlled study. J Am Geriatr Soc 2008;56:976-85. https://doi.org/10.1111/j.1532-5415.2008.01707.x
21. Smania N, Bonetti P, Gandolfi M, Cosentino A, Waldner A, Hesse S et.al. Improved gait after repetitive locomotor training in children with cerebral palsy. Am J Phys Med Rehabil 2011;90:137-49. https://doi.org/10.1097/PHM.0b013e318201741e
22. Kirkwood R, Moreira B, Vallone M, Mingoti S, Dias R, Sampaio R. Step length appears to be a strong discriminant gait parameter for elderly females highly concerned about falls: a cross-sectional observational study. Physiother 2012;97:126-31. https://doi.org/10.1016/j.physio.2010.08.007
23. Scianni A, Teixeira-Salmela L, Ada L. Effect of strengthening exercise in addition to task-specific gait training after stroke: a randomised trial. Int J Stroke 2010;5:329-35. https://doi.org/ 10.1111/j.1747-4949.2010.00449.x
24. Knikou M. Plasticity of corticospinal neural control after locomotor training in human spinal cord injury. Neural Plast 2012;2012:1-13.
25. Rhea C, Wutzke C, Lewek M. Gait dynamics following variable and constant speed gait training in individuals with chronic stroke. Gait Post 2012;36:332-4. https://doi.org/ 10.1016/j.gaitpost.2012.03.014
26. Hamill J, van Emmerik R, Heiderscheit B, Li L. A dynamical systems approach to lower extremity running injuries. Clin Biomech (Bristol, Avon) 1999;14:297-308. https://doi.org/ 10.1016/s0268-0033(98)90092-4
27. Ho C, Holt K, Saltzman E, Wagenaar R. Functional electrical stimulation changes dynamic resources in children with spastic cerebral palsy. Phys Ther 2006;86:987-1000.
28. Holt K, Fonseca S, Obusek J. Dynamic and thermodynamic constraints and the metabolic cost of locomotion. In: Sparrow W. Energetics of human activity. 1ª ed. Champaign: Human Kinetics; 2000. p. 255-85.
29. Obusek J, Holt K, Rosenstein R. The hybrid mass-spring pendulum model of human leg swinging: stiffness in the control of cycle period. Biol Cybern 1995;73:139-47. https://doi.org/10.1007/BF00204052
30. Holt K. Constraints in the emergence of preferred locomotory patterns. In: Rosenbaum DA, Collyer C. Timing of Behavior: Neural, psychological, and computational perspectives. 1ª ed. Cambridge: MIT Press; 1998. p. 261-91.
31. Holt K, Saltzman E, Ho C, Kubo M, Ulrich B. Discovery of the pendulum and spring dynamics in the early stages of walking. J Mot Behav 2006;38:206-18. https://doi.org/ 10.3200/JMBR.38.3.206-218
32. Holt K, Saltzman E, Ho C, Ulrich B. Scaling of dynamics in the earliest stages of walking. Phys Ther 2007;87:1458-67. https://doi.org/10.2522/ptj.20060299
33. Vaughan CL, Langerak NG, O´Malley MJ. Neuromaturation of human locomotion revealed by non-dimensional scaling. Exp Brain Res 2003;153:123-7. https://doi.org/10.1007/s00221-003-1635-x
34. Turvey M. Coordination. Am Psychol 1990;45:938-53.
35. Wagenaar R, van Emmerik R. Dynamics of pathological gait. Hum Mov Sci 1994;13:441-71.
36. van Emmerik R, Wagenaar R. Effects of walking velocity on relative phase dynamics in the trunk in human walking. J Biomechanics 1996;29:1175-84. https://doi.org/10.1016/0021-9290(95)00128-x
37. Lamoth C, Beek P, Meijer O. Pelvis-thorax coordination in the transverse plane during gait. Gait Posture 2002;16:101-14. https://doi.org/10.1016/s0966-6362(01)00146-1
38. Lamontagne A, Serres SJ, Fung J, Paquet N. Stroke affects the coordination and stabilization of head, thorax and pélvis during voluntary horizontal head motions performed in walking. Clin Neurophysiol 2005;116:101-11. https://doi.org/10.1016/j.clinph.2004.07.027
39. Stephenson JL, Lamontagne A, De Serres SJ. The coordination of upper and lower limb movements during gait in healthy and stroke individuals. Gait Post 2009;29:11-16. https://di.org/10.1016/j.gaitpost.2008.05.013
40. Meyns P, Gestel LV, Bruijin SM, Desloovere K, Swinnen SP, Duysens J. Is interlimb coordination during walking preserved in children with cerebral palsy? Res Dev Disabil 2012;33:1418-28. https://doi.org/10.1016/j.ridd.2012.03.020
41. Lamoth CJC, Meijer OG, Wuisman PIJM, Dieën JH, Levin MF, Beek PJ. Pelvis- Thorax coordination in the transverse plane during walking in persons with nonspecific low back pain. Spine 2002;27:E92-99.
42. Hreljac A. Effects of physical characteristics on the gait transition speed during human locomotion. Hum Mov Sci 1995;14:205-16. https://doi.org/10.1016/0167-9457(95)00017-M
43. Cavagna GA, Heglund NC, Taylor CR. Mechanical work in terrestrial locomotion: two basic mechanisms for minimizing energy expenditure. Am J Physiol 1977;233:R243-261. https://doi.org/10.1152/ajpregu.1977.233.5.R243
44. Fonseca S, Holt K, Fetters L, Saltzman E. Dynamical resources used in ambulation by children with spastic hemiplegic cerebral palsy: Relationship to kinematics, energetics, and asymmetries. Phys Ther 2004;84:344-54. https://doi.org/10.1093/ptj/84.4.344
45. Diedrich FJ, Warren Junior W. Why change gaits? Dynamics of the walk-run transition. J Exp Psychol Hum Percept Perform 1995;21:183-202. https://doi.org/10.1037//0096-1523.21.1.183
46. Jeng SF, Holt KG, Fetters L, Certo C. Self-optimization of walking in nondisabled children and children with spastic hemiplegic cerebral palsy. J Mot Behav 1996;28:15-27. https://doi.org/10.1080/00222895.1996.9941729
47. Skrotzky K. Gait analysis in cerebral palsied and nonhandicapped children. Arch Phys Med Rehabil 1983;64:291-5.
48. Lamoth CJC, Daffertshofer A, Meijer OG, Moseley GL, Wuisman PIJM, Beek PJ. Effects of experimentally induced pain and fear of pain on trunk coordination and back muscle activity during walking. Clin Biomech (Bristol, Avon) 2004;19:551-63. https://doi.org/10.1016/j.clinbiomech.2003.10.006