Rev Bras Fisiol Exerc 2021;20(4):433-42

doi: 10.33233/rbfex.v20i4.4223

ORIGINAL ARTICLE

Proposal of new symmetry and asymmetry indexes for the range of movement in older women

Proposta de novos índices de simetria e assimetria para amplitude de movimento em idosas

Marcos Raphael Pereira Monteiro¹, Levy Anthony Souza de Oliveira¹, Antônio Gomes de Resende Neto¹, Leônidas de Oliveira Neto², Elyson Ádan Nunes Carvalho¹, Marzo Edir Da Silva-Grigoletto¹

¹Universidade Federal de Sergipe, Aracajú, SE, Brazil

²Universidade Federal de Rio Grande do Norte, Natal, Brazil

Received: June 23, 2020; Accepted: April 9, 2021.

Correspondence: Marzo Edir Da Silva-Grigoletto, Av. Marechal Rondon, s/n, Jardim Rosa Elze, 49100-000 São Cristóvão SE, Brazil

Marcos Raphael Pereira Monteiro: raphaelmonteiro.fisio@gmail.com

Levy Anthony Souza de Oliveira: levyanthonysouza@gmail.com

Antônio Gomes de Resende Neto: neto.resende-edf@hotmail.com

Leônidas de Oliveira Neto: leonidasoliveiraneto@gmail.com

Elyson Ádan Nunes Carvalho: elysoncarvalho@gmail.com

Marzo Edir Da Silva-Grigoletto: medg@ufs.br

Abstract

Objective: To propose a new equation for calculating the symmetry and asymmetry indexes of the range of motion between members. Methods: Two different equations were proposed to assess symmetry and asymmetry between body members, called Limb Symmetry Index and Limb Asymmetry Index. Thus, the evaluation of 48 older women 60 to 79 years old was carried out, using a battery of tests for the range of motion, in addition to tests for the evaluation of upper and lower limbs, and the Ankle Test on the Leg Motion platform for ankle dorsiflexion. Data were analyzed using the equations proposed by the authors of the present study. Results: The equations used were applicable and effective for analyzing the range of motion symmetry and asymmetry between limbs in older women. Conclusion: The proposed equations are applicable for determining the range of motion symmetry and asymmetry between limbs in older women, using different functional tests. Therefore, this study provides subsidies to health professionals for this type of assessment.

Keywords: aging, physical functional performance, activities of daily living.

Resumo

Objetivo: Propor uma nova equação para o cálculo do índice de simetria e assimetria de amplitude de movimento entre membros. Métodos: Foram propostas duas equações distintas para avaliação de simetria e assimetria entre membros, denominadas como Índice de Simetria entre Membros e Índice de Assimetria entre Membros. Sendo assim, foi realizada a avaliação de 48 idosas com idade entre 60 e 79 anos, mediante bateria de testes para amplitude de movimento. Foram utilizados testes funcionais para avaliação em membros superiores, membros inferiores, e o Ankle Test na plataforma Leg Motion para a dorsiflexão de tornozelo. Os dados foram analisados através das equações propostas pelos autores do presente estudo. Resultados: As equações utilizadas se apresentaram aplicáveis e eficientes para análise da simetria e assimetria da amplitude de movimento entre membros em idosas. Conclusão: As equações propostas são aplicáveis para determinação de valores de simetria e assimetria de amplitude de movimento entre membros em mulheres idosas utilizando diferentes testes funcionais. Além disso, tais equações proporcionam subsídios aos profissionais da saúde para este tipo de avaliação.

Palavras-chave: envelhecimento; desempenho físico; atividades cotidianas.

Introduction

Limb asymmetry in the aging process has been related to higher chances of falling [1], gait alterations [2,3], and consequently greater functional loss. Most of the current studies evaluate this imbalance between body segments based on the difference of strength or power between limbs [1,2,3,4]; however, as well as strength, range of motion (ROM) also needs to present bilateral symmetry to ensure a good functionality of the older women. Losses in symmetry and reduction of ROM in aging are related to postural changes that can lead to functional loss of the locomotor system [5,6]. Therefore, bilateral ROM is an important variable to be evaluated, facilitating the integration of flexibility exercises in training protocols that aim to improve the health of this population [7].

In this context, symmetry and asymmetry indexes have been proposed in the literature, such as the asymmetry index (ASI) [2,8,9] and the limb symmetry index (LSM) [10], which provide information on how much a limb is asymmetrical concerning the other, either through numerical data or as a percentage. Some of these indexes use the principle of directional dominance and employ within their calculation the variable "dominant side of the body" [9,11], as applied in the following equation

ASI = 1 - (Dominant side/Non-Dominant side) × 100 [9]

Other indices start from the concept of asymmetry without direction, which does not use the dominance principle. These indexes assume that asymmetry is defined as the ratio of the difference in a given ability between the more developed and less developed sides, presenting an aspect closer to the individual's functionality [2,11].

When dealing with variables calculated through equations, it is necessary to understand that the potential of this variable is attributed to the evaluation instrument used, not to the calculation procedure, and the equation is a tool that can be used for different tests without influencing the final potential of the variable. However, when we deal with the analysis of asymmetry between the limbs, we found a range of studies that analyze the levels of strength or muscle power in various tests [12] and a scarcity of studies that enable the comparative analysis of ROM. This occurs because, in the context of ROM, the result of several tests can present negative, positive, or null scores [13,14]. These asymmetry indexes developed for strength analysis do not discriminate between positive and negative values in their equation and thus do not contemplate tests that have negative or null scores as possibilities.

By not discriminating between positive and negative values, a test that can be 10 cm negative, denoting a low ROM, can be interpreted in the equation as 10 cm positive, representing a high ROM, adding a difference of 20 cm in the total value. In addition, equations sometimes involve division processes between the values found, and by putting null values in the denominator, the equation will not be able to translate the information into numerical values. Examples of tests that are not contemplated by the equations involve the upper and lower limb ROM functional tests of the Senior Fitness Test battery [14] and the ankle dorsiflexion test in a closed kinetic chain called the Ankle Test [13].

Thus, although bilateral symmetry of mobility is considered an important factor for older women’s functionality, to our knowledge, there are no equations that support its evaluation. Thus, the current scientific literature lacks indexes that can analyze the symmetry of the ROM in a simple, applicable, easy to handle and understand way, and with equations that contemplate negative and null values. The primary objective of this study was to propose a new equation to calculate the index of symmetry and asymmetry of ROM between limbs.

Methods

This is an observational and cross-sectional study with information collected individually, with each participant being evaluated in different functional tests at a single time, which objective was the analysis of the range of motion symmetry using four different equations, two of which were original proposals by the authors of the present study, and two others already used in the scientific literature (Figure 1).

Figure 1 - Study flowchart

Sample

The study sample was drawn in a non-probabilistic way and by convenience. To this end, we used social media, advertisements in sound cars, and pamphlets. The inclusion criteria adopted, besides the expression of interest in participating in the study (by signing the consent form), were the individuals be female and between 60 and 79 years old. The exclusion criteria were: having an osteoarticular disorder that would make it impossible to perform the functional tests, as assessed by anamnesis; presenting cognitive ability attested by a score of less than 13 on the Mini Mental State Examination; and finally, complaining of pain during the tests or being unable to perform any of the tests necessary to complete the study.

Thus, 48 volunteers were selected to participate in the study, being first submitted to an interview to collect demographic variables, lifestyle habits, and variables related to health status. All participants were appropriately informed about the study's objectives and the procedures to which they would be submitted and then signed the Informed Consent Form.

Anthropometric measurements

Body mass was determined using a calibrated anthropometric scale (Filizola, São Paulo, Brazil), with a maximum capacity of 150 kg. Height was determined using a stadiometer (Sanny®, ES2030, São Paulo, Brazil).

Functional characterization

For functional evaluation, the participants were submitted to three different tests of the Senior Fitness Test battery, which were: the 8-Foot-Up-And-Go, to evaluate agility and dynamic balance; the 30-Seconds Chair Stand to estimate the strength endurance of lower limbs; the 30-Seconds Arm Curl, in both arms, to estimate the strength endurance of upper limbs; and the Six-Minute Walk test to estimate cardiorespiratory capacity [15]. The tests performed were previously correlated with other protocols already validated in the literature to assess the level of strength and cardiorespiratory capacity, showing correlation values between 0.71 and 0.78, thus meeting the criteria of validity and reliability of the use of this battery of tests, besides the easy applicability in community settings, as is the case of this study [15]. The results of the tests were expressed as mean and standard deviation to characterize the sample’s functional level, and for the 30-seconds arm curl, an average was obtained between the values of the two arms.

Ankle dorsiflexion

We used the Ankle Test on the Leg Motion® platform, which consists of a closed kinetic chain evaluation, more similar to daily life activities. The Leg Motion platform has two parts, one that supports the individual's feet and another with a measuring rod with a scale in centimeters. During the evaluation, the individual remained in bipedal support, with one foot on the platform and the other foot behind it. The subject was asked to perform maximum ankle dorsiflexion to bring the knee to the measuring rod, which was adjusted according to the lower border of the patella’s height. The test was done with both limbs, with two attempts for familiarization and one for data analysis. The attempt was considered invalid if the subject removed the heel from the ground [13].

Range of motion of the upper limbs

To evaluate the range of motion of the upper limbs was used the Back Scratch test. The procedure asks the patient to stand up and perform a movement of placing her hand on her back, performing shoulder abduction, elbow flexion, forearm pronation, and keeping the fingers extended, trying to reach the greatest possible amplitude, going towards the hips. The other hand is also positioned on the back, but performing shoulder adduction, elbow flexion, forearm supination, and fingers extension, trying to reach the greatest possible amplitude, going towards the head. Assumed this position, the goal of the test was to bring the hands as close as possible, and the side to be evaluated is the shoulder that performs abduction. After the evaluator's demonstration, the participant made two attempts with both sides, and the best score in each action was chosen as the result. The distance between the middle fingers was measured in centimeters. In this test, the final score can be presented as positive values, when one limb exceeds the other; negative values, when one limb does not reach the other; or null, when the result is the meeting point between the two limbs [15].

Range of motion of the lower limbs

To assess the range of motion of the lower limbs, we used the Chair Sit-And-Reach test, which is performed as follows: initially, the patient sits on the edge of a chair, with the limb to be evaluated with knee extension and ankle in the neutral position, and then to slowly lower the trunk with the upper limbs in elbow extension, hands overlapped and shoulders directed perpendicular to the hallux. Meanwhile, the contralateral leg remained with the knee flexed at 90 degrees. For this test’s scoring, the tip of the hallux corresponded to the zero point; if this point was not reached, the result was negative (missing distance to the hallux), and if it was exceeded, the result was positive (distance reached after the hallux). The test was done for both lower limbs, and attempts were considered invalid if the subject flexed the knee of the assessed limb. Two attempts were performed, and the best score was chosen for further analysis [15].

Proposed indexes

To evaluate the symmetrical relations between the limbs, two indexes proposed by the authors were used, with the purpose that their equations can contemplate all possible values to be provided by the tests, being these negative, positive, or null. The first index was the Limb Symmetry Index (ISM), which uses the modulus of the difference between the right limb and the left limb and divides it by a reference value established as

The second index used was the Limb Asymmetry Index (IAM), which follows the same reasoning as the ISM, but offers the value of asymmetry

Statistical analysis

The data were expressed according to their mean and standard deviation, and for comparison between members were used the two different equations of ISM and IAM, previously presented. For both indexes, we calculated the Coefficient of Variation

and the Minimum Detectable Difference

In addition, was made an example formulation for better understanding when we used the ISM and IAM equations proposed by the authors of this study and two other distinct equations already used in the literature [9,16]. The third equation refers to an asymmetry index that considers the strong side and weak side which for didactic purposes we will call here ASI¹:

ASI = 1 - (Strong Side/Weak Side) × 100 [9]

The fourth equation is another asymmetry index that considers the dominant side and non-dominant side which we will call ASI².

[16]

Results

Table I shows the sample characterization with data regarding age, anthropometric tests, and physical capacity. Based on the normative scores for older Brazilian women between 60 and 69 years old, the data of upper limbs strength, lower limbs strength, and cardiorespiratory capacity are above the average, while the scores referring to dynamic balance and agility are below the average [17]. Considering the average age of the group and according to the normative scores of physical fitness for older Brazilian women between 60 and 64 years old, we can notice that the average scores for agility and dynamic balance are close to the 70 percentile, for the lower limbs strength, close to the 60 percentile, for the upper limbs strength, close to the 55 percentile, and for functional resistance, close to the 65 percentile [17].

Table I - Anthropometric and morphofunctional characteristics of the sample. Information presented as mean ± standard deviation

BMI = Body Mass Index

Tables II and III show the symmetry and asymmetry values, using the ISM and IAM equations. Table II shows the values according to the symmetry index between members developed by the authors, and Table III shows the values obtained according to the asymmetry index between members.

Table II - Symmetry values according to the Limb Symmetry Index (ISM). Values expressed in percentage

SD = Standard Deviation; CV = Coefficient of Variation; MDD = Minimum Detectable Difference

Table III - Asymmetry values obtained according to the Limb Asymmetry Index (IAM). Values expressed in percentage

SD = Standard Deviation; CV = Coefficient of Variation, MDD – Minimum Detectable Difference

Finally, in Table IV, we present the evaluation of ten imaginary individuals for didactic example, using the Back Scratch test with the same dominant limb for all participants and their respective symmetry and asymmetry calculations using the equations of LAI, LSM, ASI1, and ASI2.

Table IV - Values by the calculation of symmetry and asymmetry with different equations

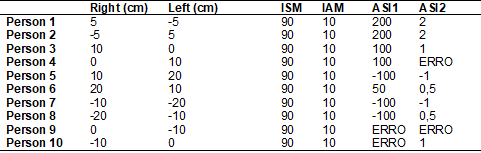
LSI = Limb Symmetry Index; LAI = Limb Asymmetry Index; ASI1 = Asymmetry index that considers strong side and weak side; ASI2 = Asymmetry Index that considers dominant and non-dominant side

Discussion

The main findings of this study infer that the proposed equation has good applicability for range of motion tests that use measurements expressed in positive, negative, and null scores, aiming at determining the indexes of symmetry or asymmetry between limbs.

Thus, when we compare the equation presented to indexes already used in the literature for strength evaluation, we can notice certain particularities that attest to its advantages over the others. To demonstrate the deficits found in the other equations, we used the example shown in Table IV, which represents a situation close to reality, in which a test used in a certain population can present positive, negative, or null scores.

In this example, all individuals have a similar degree of symmetry and asymmetry between limbs, and all have right limb dominance. In all individuals, the asymmetry is 10 cm between the limbs. However, we can notice that the equations proposed by the authors keep the same result, while the other equations do not present accuracy to identify the result for all individuals.

In turn, the two asymmetry equations proposed in the literature, ASI1 and ASI2 [9,16], cannot analyze null values, not being applicable in conditions that present 0 as a possible score, besides not recognizing negative values according to the order in which they are presented in the equation. The second also requires the need for knowledge of member dominance for its applicability; this becomes one more factor to be recorded during the research, besides not expressing the concept of asymmetry without direction [2].

Among the advantages of the proposed equations is the fact that they do not involve the principle of dominance, since the dominant side can be determined in different subjective ways, as in the case of lower limbs that can be determined by the leg used to recover balance after a disturbance [11] or the self-determined foot to climb a staircase [18]. For this, the ability level of each limb in the test is considered, ensuring that in the subtraction of right and left, the value is always absolute. This measure has a more functional character over symmetry, as it works with the physiological deficit between the limbs [2].

It is important to emphasize that the sample assessed presented scores for physical capacity tests like the normative scores established for this population in Brazil and United States [19]. Thus, the equations proposed here are based on usual data, easily found in the daily routine of the professional who works with movement.

The present study results must be interpreted with caution since we can point out some limitations, such as the absence of sample size calculation for the study and the impossibility of the proposed equations to define which limb reached higher scores when compared to the other.

In conclusion, the Limb Symmetry Index (ISM) and the Limb Asymmetry Index (IAM), both proposed by the present study authors, are applicable and efficient for determining the values of symmetry and asymmetry of range of motion between limbs, using different functional tests. As future perspectives, it is recommended to test them in different populations, such as in older men.

Conclusion

The results of this investigation provide subsidies to health professionals to evaluate the symmetry of range of motion between limbs in a simple, applicable, easy to handle, and understandable manner, considering tests that have the possibility of positive, negative, and null scores.

Conflict of interest

No conflict of interest with relevant potential.

Financing source

This study was financed in part by the Fundação de Apoio à Pesquisa e à Inovação Tecnológica do Estado de Sergipe (FAPITEC/SE).

Author’s contributions

Conception and design of study: Monteiro MRP, Silva-Grigoletto ME; Acquisition, analysis and/or interpretation of data: Monteiro MRP, Oliveira LAS, Neto AGR, Carvalho EAN; Drafting the manuscript: Monteiro MRP; Revising the manuscript critically for important intellectual content: Oliveira LAS, Neto AGR, Neto LO, Carvalho EAN, Silva-Grigoletto ME.

References

1. Skelton DA, Kennedy J, Rutherford OM. Explosive power and asymmetry in leg muscle function in frequent fallers and non-fallers aged over 65. Age Ageing 2002;31(2):119-25. doi: 10.1093/ageing/31.2.119 [Crossref]
2. Koda H, Kai Y, Murata S, Osugi H, Anami K, Fukumoto T, et al. Relationship between muscle strength asymmetry and body sway in older adults. J Aging Phys Act 2018;26(3):457-61. doi: 10.1123/japa.2017-0096 [Crossref]
3. Laroche DP, Cook SB, Mackala K. Strength asymmetry increases gait asymmetry and variability in older women. Med Sci Sports Exerc 2012;44(11):2172-81. doi: 10.1249/mss.0b013e31825e1d31 [Crossref]
4. LaRoche DP, Villa MR, Bond CW, Cook SB. Knee extensor power asymmetry is unrelated to functional mobility of older adults. Exp Gerontol 2017;98:54-61. doi: 10.1016/j.exger.2017.08.008 [Crossref]
5. Tashiro M, Honda Y, Ohkubo M, Sugiyama T, Ishida R. Influence of cervical, thoracic and lumbar spines, and shoulder girdle range of motion on swallowing function of dependent older adults. Geriatr Gerontol Int 2017;17(12):2565-72. doi: 10.1111/ggi.13097 [Crossref]
6. Drzal-Grabiec J, Snela S, Rykala J, Podgorska J, Banas A. Changes in the body posture of women occurring with age. BMC Geriatr 2013;13:108. doi: 10.1186/1471-2318-13-108 [Crossref]
7. Bray NW, Smart RR, Jakobi JM, Jones GR. Exercise prescription to reverse frailty. Appl Physiol Nutr Metab 2016;41(10):1112-6. doi: 10.1139/apnm-2016-0226 [Crossref]
8. Carabello RJ, Reid KF, Clark DJ, Phillips EM, Fielding RA. Lower extremity strength and power asymmetry assessment in healthy and mobility-limited populations: reliability and association with physical functioning. Aging Clin Exp Res 2010;22(4):324-9. doi: 10.1007/bf03337729 [Crossref]
9. Fort-Vanmeerhaeghe A, Gual G, Romero-Rodriguez D, Unnitha V. Lower limb neuromuscular asymmetry in volleyball and basketball players. J Hum Kinet 2016;50:135-43. doi: 10.1515/hukin-2015-0150 [Crossref]
10. Xergia SA, Pappas E, Zampeli F, Georgiou S, Georgoulis AD. Asymmetries in functional hop tests, lower extremity kinematics, and isokinetic strength persist 6 to 9 months following anterior cruciate ligament reconstruction. J Orthop Sports Phys Ther 2013;43(3):154-62. doi: 10.2519/jospt.2013.3967 [Crossref]
11. Hewit JK, Cronin JB, Hume PA. Asymmetry in multi-directional jumping tasks. Phys Ther Sport 2012;13(4):238-42. doi: 10.1016/j.ptsp.2011.12.003 [Crossref]
12. Bishop C, Read P, Chavda S, Turner A. Asymmetries of the lower limb: The calculation conundrum in strength training and conditioning. Strenght Cond J 2016;38(6):27-32. doi: 10.1519/SSC.0000000000000264 [Crossref]
13. Calatayud J, Martin F, Gargallo P, Garcia-Redondo J, Colado JC, Marin PJ. The validity and reliability of a new instrumented device for measuring ankle dorsiflexion range of motion. Int J Sports Phys Ther 2015;10(2):197-202.
14. Rikli RE, Jones CJ. Development and validation of a functional fitness test for community-residing older adults. J Aging Phys Act 1999;7(2):129-61. doi: 10.1123/japa.7.2.129 [Crossref]
15. Rikli RE, Jones CJ. Development and validation of criterion-referenced clinically relevant fitness standards for maintaining physical independence in later years. Gerontologist 2013;53(2):255-67. doi: 10.1093/geront/gns071 [Crossref]
16. Hadzic V, Sattler T, Veselko M, Markovic G, Dervisevic E. Strength asymmetry of the shoulders in elite volleyball players. J Athl Train 2014;49(3):338-44. doi: 10.4085/1062-6050-49.2.05 [Crossref]
17. Mazo GZ, Petreça DR, Sandreschi PF, Benedetti TRB. Valores normativos da aptidão física para idosas brasileiras de 60 a 69 anos de idade. Rev Bras Medicina do Esporte 2015;21(4):318-22. doi: 10.1590/1517-869220152104134470 [Crossref]
18. Ceroni D, Martin XE, Delhumeau C, Farpour-Lambert NJ. Bilateral and gender differences during single-legged vertical jump performance in healthy teenagers. J Strength Cond Res 2012;26(2):452-7. doi: 10.1519/jsc.0b013e31822600c9 [Crossref]
19. Krause MP, Januário RS, Hallage T, Haile L, Miculis CP, Gama MP, et al. A comparison of functional fitness of older Brazilian and American women. J Aging Phys 2009;17(4):387-97. doi: 10.1123/japa.17.4.387 [Crossref]