Rev Bras Fisiol Exerc 2021;20(3):346-57
doi: 10.33233/rbfex.v20i3.4623
ORIGINAL ARTICLE
Differences in the load-velocity relationship between
untrained men and women during the back squat exercise
Diferenças
na relação carga-velocidade entre homens e mulheres destreinados durante o back squat
Levy
Anthony de-Oliveira1, Fernando Martín-Rivera2, Marzo Edir
Da Silva-Grigoletto1
1Universidade Federal de Sergipe, São
Cristóvão, Brasil
2Universitat de València,
València, Espanha
Received:
March 16, 2021; Accepted:
April 15; 2021.
Correspondence: Marzo Edir Da Silva-Grigoletto,
Rua Prof. Arício Guimarães Fortes, 321/902, 49037-060
Aracaju SE
Levy Anthony de-Oliveira: levyanthonysouza@gmail.com
Fernando Martín-Rivera: f_martin_r@yahoo.es
Marzo Edir Da Silva-Grigoletto:
medg@ufs.br
Abstract
Objectives: The purposes
of this investigation were: 1) to compare the load-velocity relationship
estimated by the two-point method between untrained men and women during the
parallel back squat exercise (BS) and 2) to compare the load-velocity profile
found in our study with the load-velocity profiles reported in the scientific
literature for trained individuals. Beyond, we aimed to compare the measured
1RM velocity with predicted 1RM velocity by the two-point method in the BS
exercise in untrained individuals. Methods: Seventy-six untrained
individuals (38 men (22.7 ± 4.4 years; 174.9 ± 6.8 cm; 76.1 ± 14.9 kg) and 38
women (24.7 ± 4.3 years; 159.1 ± 6.0 cm; 64.7 ± 13.3 kg) performed a
one-repetition maximum test and a progressive two-load test with 20% 1RM and
70% 1RM to estimate their load-velocity relationships. Results: The main
results revealed that 1) mean propulsive velocity and mean velocity attained at
each relative load were different between men and women (p < 0.05). However,
the measured 1RM velocity was not significantly different between them.
Untrained men provided a steeper load-velocity relationship than women. We
found that 2) untrained individuals of our study showed a different
load-velocity profile than trained individuals from scientific literature
studies. Furthermore, 3) the measured 1RM velocity was lower than the predicted
1RM velocity (p < 0.05). Conclusion: These results suggest that the
load-velocity relationship is dependent on sex and training background, and the
two-point method using 20% and 70% 1RM might not be reliable to estimate the
load-velocity relationship in the BS exercise for untrained men and women.
Keywords: exercise; velocity measurement;
muscle strength.
Resumo
Objetivos: Os objetivos deste estudo foram: 1)
comparar a relação carga-velocidade estimada pelo método de dois pontos entre
homens e mulheres destreinados durante o exercício agachamento paralelo (BS) e
2) comparar o perfil carga-velocidade encontrado em nosso estudo com os perfis
de carga-velocidade relatados na literatura científica para indivíduos
treinados. Além disso, comparar a velocidade de 1RM medida com a velocidade de
1RM predita pelo método de dois pontos no exercício BS em indivíduos
destreinados. Métodos: Setenta e seis indivíduos destreinados (38 homens
(22,7 ± 4,4 anos; 174,9 ± 6,8 cm; 76,1 ± 14,9 kg) e 38 mulheres (24,7 ± 4,3
anos; 159,1 ± 6,0 cm; 64,7 ± 13,3 kg) realizaram um teste de uma repetição
máxima e um teste progressivo de duas cargas com 20% e 70% 1RM para estimar
suas relações carga-velocidade. Resultados: Os principais resultados
revelaram que 1) a velocidade média propulsiva e a velocidade média atingida em
cada carga relativa foram diferentes entre homens e mulheres (p < 0,05). No
entanto, a velocidade de 1RM medida não foi significativamente diferente entre
eles. Homens destreinados forneceram uma relação carga-velocidade mais
acentuada do que as mulheres. Descobrimos que 2) os indivíduos destreinados de
nosso estudo apresentaram um perfil carga-velocidade diferente dos indivíduos
treinados dos estudos da literatura científica. Além disso, 3) a velocidade de
1RM medida foi menor do que a velocidade de 1RM predita (p < 0,05). Conclusão:
Esses resultados sugerem que a relação carga-velocidade é dependente do sexo e
treinamento, e que o método de dois pontos usando 20% e 70% 1RM não seria
confiável para estimar a relação carga-velocidade no exercício agachamento
paralelo em homens e mulheres destreinados.
Palavras-chave: exercício; mensuração da velocidade;
força muscular.
Introduction
The one-repetition
maximum (1RM) value is the primary reference for prescribing training loads in
resistance training [1]. The classical way to assess it is through the trial-and-error
method, directly measuring the 1RM load [2]. As this method has essential
drawbacks [3], researchers tried to determine the 1RM load through indirect
methods [4,5,6]. However, indirect methods pursue relevant limitations as well
[3]. The movement velocity measuring during resistance exercises gained
popularity in the field of strength and conditioning to avoid these methods'
limitations as almost perfect relationships were found between the magnitude of
the load and the bar velocity in many resistance exercises [7,8,9,10,11]. In this
regard, generalized regression equations have been proposed to determine
relative load (%1RM) and the 1RM load [8,12].
The generalized
group equations also have some critical limitations [13]. It assumes that the
load-velocity relationship is exercise-specific, i.e., each exercise has its
1RM velocity (V1RM). In this way, the velocity of each % 1RM is treated as been
equal for all individuals. Recent studies have observed that the load-velocity
relationship is individual, suggesting using an individualized load-velocity
relationship for a more accurate 1RM prediction [14,15]. Furthermore, there is
also a possibility that the training level of the individuals influences the
load-velocity relationship once it is well known that untrained individuals
pursue different nervous system integration and insufficient ability of the
nervous system to activate the muscles appropriately [16]. As the movement
velocity is a consequence of the muscle force applied, and the muscle force
applied is a consequence of muscle activation and coordination, different
muscle activation patterns could lead to different velocities outputs. Besides
that, the higher rate of strength gain of untrained individuals could influence
the velocities outputs as those individuals still can achieve a much better
neuromuscular performance [17]. It would be interesting to evaluate untrained
and trained individuals' load-velocity profiles to test this hypothesis.
Another
limitation of the generalized group equations is that the load-velocity profile
is sex-specific [14]. Recently, Torrejón et al.
[18] found that the load-velocity profile differs more between men and women
than between individuals with different strength levels in the bench press
exercise. Balsalobre-Fernández et al. [7]
showed that women develop velocities with each %1RM lower than men in the
military press exercise. Based on our knowledge, only one scientific study [4]
verified the load-velocity relationship in untrained men and women in a
lower-body exercise, the back half-squat. However, recent solid evidence [19]
suggested that the use of the half-squat exercise is inconvenient. This study
indicated limited performance improvements, pain and discomfort increments
after half-squat training and the use of parallel or full squat exercise was
recommended. Thus, it will be pertinent to provide a detailed description of
the load-velocity relationship in untrained men and women in an effective squat
exercise.
Furthermore, the
two-load method has emerged as an alternative method to the traditional
load-velocity testing with multiple loads. The multiple-load method consists of
the velocity measurement against several external loads (usually 4-9 loads) at
varying progressive intensities. In this way, it can be prone to fatigue,
time-consuming, and impractical on a daily basis and
for large groups [13,20]. In this regard, assuming that the load-velocity
relationship is generally stable and linear in resistance exercises, the
two-load method only analyses two loads [13]. Recent study [21] found that the
two-load method is optimal because of the higher validity and similar
reliability observed than the multiple-load method [13]. Although the two-point
method is reliable for determining the load-velocity relationship and
predicting the 1RM, it has been analyzed after applying the multiple-load
method. In this regard, this method should be analyzed separately from the
multiple-load method because the fatigue accumulated through several loads
could affect the velocity output [13].
Therefore, our
purposes were 1) to estimate and compare the load-velocity relationship between
untrained men and women and 2) to compare the load-velocity relationship found
in our study with those found in the scientific literature for trained
individuals in the parallel back squat exercise (BS) to know if the training
level influences the load-velocity relationship. Besides that, we aimed 3) to
assess if the measured V1RM is like the predicted V1RM from the load-velocity
relationship estimated by the two-point method in the BS exercise in untrained
individuals.
Methods
Experimental design
A
cross-sectional study was designed to meet the objectives described above. The
participants reported to the laboratory on three occasions, separated by at
least 48-72 hours. This study's independent variable was the %1RM, and the
dependent variable was the velocity attained at each %1RM. During the first
session, height and body mass were measured, and familiarization with BS was
performed. During the second session, the individual 1RM for the BS was
established. In the third session, we estimated the load-velocity relationship
through the two-load method. To control the influence of external factors
possibly affecting exercise performance, all the sessions were controlled by
the same two investigators, certified strength, and conditioning specialist
(CSCS), and were conducted in the physiology laboratory in the Physical Education
Department at the Federal University of Sergipe, under similar environmental
conditions (~23° C; ~60% humidity).
Participants
Seventy-six (38
men and 38 women) untrained individuals volunteered to participate in this
research study. Men (22.7 ± 4.4 years; 174.9 ± 6.8 cm; 76.1 ± 14.9 kg) and
women (24.7 ± 4.3 years; 159.1 ± 6.0 cm; 64.7 ± 13.3 kg). All of them had a
minimum of one year of resistance training experience with the BS, but they
were untrained for at least three months at the time of the study. All
participants were free from musculoskeletal pain, neuromuscular disorders, or
any form of joint or bone disease that could compromise the test performance.
None of the participants took drugs, medications, or other substances to alter
their physical performance during the tests. Participants were informed of the
study procedures, risks, and benefits. They read and signed a written informed
consent form before initiating the study. The study procedures were approved by
the Federal University of Sergipe Institutional Review Board (CAAE:
23629619.4.0000.5546).
Familiarization
with the BS exercise
After a
standardized dynamic warm-up (the warm-up was the same for all the sessions),
which each participant performed 5 min of joint mobility, followed by two sets
of 15 and 10 repetitions (interspaced with 2 min rest) with external loads of
10 and 20 kg for women, 20 and 30 kg for men respectively of the BS. The
participants were familiarized with the proper technique of the BS. The
movement started from an upright position (point A), with hips and knees fully
extended. The bar was grasped with a pronated grip and rested across the back
on the trapezius's upper part. The stance was approximately shoulder-width
apart, parallel feet flat on the floor or externally rotated to a maximum of
15°. From this position, participants descended in a controlled motion until
the inguinal crease reached (point B) the same horizontal plane as the superior
border of the patella [10,22]. After a momentary pause (~1.5 s), they ascended
back to the upright position while keeping an upright straight trunk posture
[23].
1RM strength testing
In the second
session, after the dynamic warm-up described above, the 1RM BS load was
measured according to the protocol established by Pareja-Blanco et al. [24].
The BS technique performed was the same as described above. Once the subjects
reached point B of the BS, the bar's distance to the ground was measured to
establish the BS's depth. The bar displacement was measured with the linear
position transducer cited behind to ensure that the subjects performed a
similar depth at each BS repetition. A limit of 10% bar displacement loss was
established since the loads were increased, and if this criterion was not attended,
a new trial was made after a 5 min rest.
Two-load method
In the third
session, the individual load-velocity relationship was estimated using a
progressive two-load test. Before the commencement of the load-velocity test,
participants performed the same standardized warm-up mentioned above. After
warming up, the BS exercise bar velocity in the Smith machine was measured
against two loads, 20% and 70% 1RM measured in the second session. The BS's
eccentric phase was executed at a controlled mean bar velocity (~0.50-0.70
m.s-1) to ensure standardization and security during the lift. Participants
were instructed to move as fast as possible during the concentric phase. Strong
verbal encouragement was provided to the individuals to reach maximal intended
velocity. One set against each load was performed, and five to three
repetitions were executed. The set was stopped when the bar velocity decreased
in two consecutive reps. If the same bar displacement was not replicated or the
controlled bar velocity during the eccentric phase was not achieved, a new set
was made after 3 minutes rest [25]. The fastest repetition of the BS at each
load was considered for the analysis.
Measurement equipment and data analysis
Height (cm) and
body mass (kg) were measured using a stadiometer (Sanny,
ES2030, São Paulo, Brazil), with an accuracy of 0.1 cm and an anthropometric
scale (Líder®, P150C, São Paulo, Brazil) with a
maximum capacity of 150 kg respectively. These
variables were measured according to procedures described elsewhere [26]. A
Smith Machine (Technogym, Gambetola-Italy) was used
for all the BS performed. Velocity data was measured with a linear position
transducer (LPT) with a frequency of 1,000 Hz (Chronojump
®, Boscosystem, Barcelona-Spain). The bar displacement
and velocity were automatically calculated by the custom software v.1.9.0. The
validity and reliability of this device have been previously reported [27,28].
Mean velocity
(MV) and mean propulsive velocity (MPV) for each exercise's repetition were
obtained. The MV is the average velocity of the whole concentric phase of the
BS. The MPV is the average velocity of the BS's propulsive phase. The
propulsive phase is the portion of the concentric phase that occurs until the
braking phase. When the measured acceleration [a] is greater than the
acceleration due to gravity, i.e., a ≥- 9.81 m.s-2
[13,25].
Statistical analyses
Descriptive data
are presented as mean, standard deviation, and 95% confidence intervals (CI).
The Kolmogorov-Smirnov test confirmed the normal distribution of the data.
Linear regression analyses were used to describe the load-velocity
relationships to estimate the relative load from the bar velocity. An
independent t-test was used to compare the velocities against 20-100% 1RM
between untrained men and women. One sample t-test was used to compare
anthropometric measures, relative and absolute strength, MPVs, and MVs of our
study with, on our knowledge, all the studies of the scientific literature that
verified the load-velocity relationship for the parallel BS exercise with
trained individuals. We calculated paired t-test to determine the goodness of
the two-point method to estimate the V1RM, comparing the velocity of the
directly measured 1RM with the estimated V1RM. Cohen's d effect size (ES) was
measured to determine the magnitude of the mean differences. The interpretation
of the ES was as follows: trivial (< 0.20), small (0.20-0.59), moderate
(0.60-1.19), large (1.2-2.0) and very large (> 2.0) effect [29]. The level
of significance was established at p < 0.05. Statistical analyses were
performed using Graphpad Prism 8.0.2 (GraphPad
Software Inc., La Jolla, CA, USA).
Results
1RM Back Squat
The measured 1RM
value of the BS for men and women was 100 ± 22 kg (i.e., 1.34 ± 0.28 per kg of
body mass) and 63 ± 16 kg (i.e., 0.98 ± 0.29 per kg of body mass),
respectively. Untrained men lifted a higher 1RM load than untrained women (p
< 0.05).
Comparison of load-velocity relationships between
untrained men and women
Table I shows
that estimated MPV and MV attained at each relative load (20-100%, with 10%
increments) were different between men and women (p < 0.05). Untrained men
achieved higher velocity values at each % 1RM, providing a steeper
load-velocity relationship than untrained women. However, the measured V1RM was
not significantly different between them (Table I).
One sample
t-test showed quite similar (p > 0.05) anthropometric measures, absolute and
relative strength of our sample compared with the trained male of Martínez-Cava
et al. study [10] (Table II). When compared with the NCAA Division I
baseball athletes of Spitz et al. study [30], there was statistical differences
between untrained men of our study and the athletes of their study (Table II).
The athletes were younger, taller, bigger, and stronger than our sample. We
found that our study's untrained individuals showed a different load-velocity
profile than trained individuals of Martínez-Cava et al. [10] and Spitz et al.
[30] studies (Table III). Untrained men of this study achieved higher
velocities than trained men of the Martínez-Cava et al. study [10].
Spitz et al. [30] analyzed only four relative loads. Our study's
untrained men attained lower velocities with 30%, 50%, and 70% 1RM loads
compared with their study. However, the velocity of 90% 1RM was similar between
us and their study.
V1RM prediction through the two-point method
Table I shows
that the measured V1RM was significantly different from predicted 1RM MPV for
men (ES = 2.83) and women (ES = 2.54), and for predicted 1RM MV for men (ES =
4.12) and women (ES = 2.90). The measured 1RM velocities were smaller than the
predicted 1RM velocities for both sexes.
Table I - Mean
propulsive velocity (MPV) and mean velocity (MV) attained with 20-100% 1RM in
the parallel back squat exercise estimated through the two-load method for the
untrained men and women
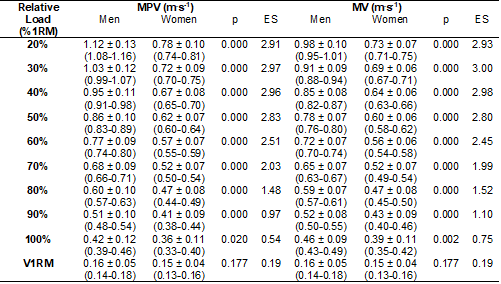
Values are mean ± SD
(95% confidence interval); p = p-value; ES = Cohen’s d effect size; V1RM =
measured 1RM velocity
Table II - Anthropometric
and muscular strength measures comparison between untrained men of our study
and trained men of Martínez-Cava et al. [10] and male NCAA Division I baseball
position players of Spitz et al. [30] studies

Values are mean ± SD; *
= significantly different from our study (p < 0.001); ES = Cohen's d effect
size
Table III - Mean
propulsive velocity (MPV) and mean velocity (MV) differences in the parallel
back squat exercise for trained and untrained men from this study and
Martínez-Cava et al. [10] and Spitz et al. [30] studies
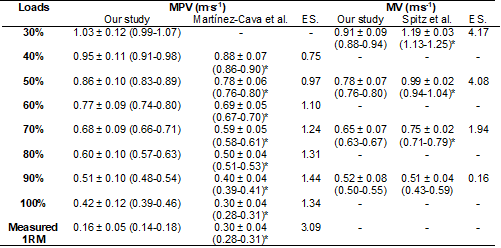
Values are mean ± SD
(95% confidence interval); * = significantly different from our study (p <
0.001); ES = Cohen's d effect size
Discussion
This study's
main findings were the different load-velocity relationships and the similar
measured V1RM found between untrained men and women, besides the different
load-velocity relationships between untrained men of our study and trained men
in previous studies. This finding suggests that the load-velocity relationship
is sex- and training level-dependent. Higher velocities with the same %1RM were
found for men compared with women during the BS. Untrained and trained
individuals showed different load-velocity profiles. As the measured V1RM was
different from the estimated V1RM through the two-point method with 20% and
70%1RM, this result might suggest that the two-point load method applied
separately does not predict the V1RM accurately for the BS. These results
provide novel information for strength and conditioning professionals that use
the velocity-based resistance training approach.
Assessing the
first aim of this study, we observed that men attained higher velocities than
women with a large and very large difference until 80%1RM. However, when
getting closer to the 1RM load, the differences were small and moderate. When
we look at the measured velocities, men attained higher velocities than women
at submaximal loads (20 and 70%1RM), but at the maximal load (1RM), the
velocities attained between sexes were similar. Previous studies [7,14] also
have found this pattern in upper-body pushing
resistance exercises like the bench press and military press. In contrast, Torrejón et al. [18] verified different measured V1RM
between trained men and women. However, it was observed in all studies cited
above a steeper load-velocity relationship for men when compared with women.
This study verified the same finding with the BS exercise (Table I). Therefore,
this suggests that the load-velocity relationship is also sex-specific, even
for the BS.
Interestingly,
the previous studies cited above assessed the load-velocity relationship in
trained men and women through the multiple-load method. Knowing that the
distance between the loads is more important than the number of loads to
determine the load-velocity relationship accurately [20]. This study used the
two-load method, and a similar pattern was observed in the load-velocity
relationship of untrained men and women for a lower-body resistance exercise.
To our knowledge, this is the first study that used the two-load method
separately. With this method, the goodness of fit cannot be verified, as only
two points are used. However, this still provides valid information due to the
many studies showing the load-velocity relationship is
linear.
Regarding
the second aim of this study, Martínez-Cava et al. [10] only verified the MPV,
whereas Spitz et al. [30] only analyzed MV and peak velocity. In this way,
untrained men showed a different load-velocity relationship than trained men.
Interestingly, when we compared our results with the Martínez-Cava et al. [10]
study, the individuals of both studies pursued very similar anthropometric and
strength values, with small differences. Furthermore, the MPV of a % 1RM in
untrained men was 10%1RM higher than trained men (Table III). Trained men
showed a deficit of ~0.10 m.s-1 when compared with their untrained
counterparts. However, we observed a higher interindividual variability in this
study. These findings can be explained by the neuromuscular differences between
untrained and trained individuals. Untrained have a limited ability to recruit
motor units, especially fast-twitch motor units maximally. They are unable to
activate all available muscle fibers successfully. Research has shown that only
71% of muscle tissue is activated during maximal efforts in this population
[31,32]. This result can cause a higher interindividual variability in
untrained individuals and the difference between populations analyzed.
Spitz et al.
[30] analyzed only four %1RM. When we compared the male athletes of their
study, we observed moderate, large, and very large differences in the
anthropometric and strength values. We found a large and very large difference
for the MV attained at 30, 50, and 70%1RM between studies samples. However, a
trivial difference of the MV at 90%1RM was found. This result was not found in
the Martínez-Cava et al. [10] study. However, Spitz et al. [30]
used only four loads in the multiple-load method, while Martínez-Cava et al.
[10] used, on average, double loads (8.8 ± 1.7 loads). This result suggests
that the number of loads influences the velocity output with the fatigue
accumulated through several loads being tested. Future studies should analyze
the two-point method separately from multiple loads to further elucidate its
accuracy in determining the load-velocity relationship.
Regarding the
third aim of this study, we implemented the two-load method to assess if the
fatigue accumulated through multiple loads being tested influences the V1RM
estimation. To assess if the two-point method could predict the V1RM with
accuracy, we compared the measured V1RM with the predicted V1RM. We found a
very large difference between these velocities suggesting that the two-load
method applied separately with 20% and 70% 1RM does not predict the V1RM accurately.
We chose these relative loads, as two distant pairs of loads should be applied
to maximize the two-point method's reliability and validity [21]. Beyond, it
was observed a higher validity and similar reliability than the multiple-load
method [21]. Therefore, the present study's result suggests that the movement
velocity output is method-dependent, which might suffer the influence of the
accumulated fatigue with multiple-loads tested.
This finding
strengthens the need that future studies should analyze the two-point method
separately from multiple loads to elucidate its accuracy for load-velocity
relationship estimation and 1RM load prediction. Future studies should also
investigate the best relative loads used during the two-point load method to estimate
the load-velocity relationship with a high degree of accuracy.
Conclusion
In conclusion,
untrained men pursue a steeper load-velocity relationship compared to untrained
women, and the load-velocity relationship is different between trained and untrained
males in the BS. Besides that, the movement velocity output is dependent on the
method used to estimate the load-velocity relationship in untrained
individuals, as the two-point method with 20% and 70% 1RM applied separated
from the multiple-load does not estimate the V1RM accurately in the BS. Thus,
the load-velocity relationship is dependent on sex, training background, and
method estimation, suggesting that researchers and strength and conditioning
professionals should take care when estimating the load-velocity relationship
and implementing the velocity-based resistance training approach in untrained
men and women using the BS.
Conflict of interest
The authors reported no
potential conflict of interest. The authors funded this research.
Author contributions
Conception and design of the research: de-Oliveira LA.
Data collection: de-Oliveira LA. Data analysis and interpretation: de-Oliveira LA, Martín-Rivera F, Da-Silva Grigoletto ME. Statistical analysis: de-Oliveira LA. Obtaining financing: N/A. Writing of the manuscript: de-Oliveira LA. Critical review of the manuscript regarding important intellectual content: Martín-Rivera F, Da-Silva Grigoletto ME.
We would like to thank
all the participants who selflessly participated in the study and the strength
and conditioning specialists from our research group who helped in the data
collection.
References
- Fry AC. The role of resistance exercise intensity on
muscle fibre adaptations. Sports Med
2004;34(10):663–79. doi: 10.2165/00007256-200434100-00004 [Crossref]
- Brown LE, Weir JP. ASEP procedures recommendation I:
accurate assessment of muscular strength and power. J Exerc
Physiol 2001;4(3):1-21.
- González-Badillo JJ, Sánchez-Medina L. Movement
velocity as a measure of loading intensity in resistance training. Int J Sports
Med 2010;31(05):347-52. doi: 10.1055/s-0030-1248333 [Crossref]
- Bazuelo-Ruiz
B, Padial P, García-Ramos A, Morales-Artacho AJ, Miranda MT, Feriche
B. Predicting maximal dynamic strength from the load-velocity relationship in
squat exercise. J Strength Cond Res 2015;29(7):1999-2005.
- Brzycki M. Strength testing-predicting a one-rep max from reps-to-fatigue. J Phys Educ Recreat Dance 1993;64(1):88-90. doi: 10.1055/s-0030-1248333 [Crossref]
- Picerno P, Iannetta D, Comotto S, Donati M, Pecoraro F, Zok M, et al. 1RM prediction: a novel methodology based on the force-velocity and load-velocity relationships. Eur J Appl Physiol 2016;116(10):2035-43. doi: 10.1007/s00421-016-3457-0 [Crossref]
- Balsalobre-Fernández C, García-Ramos A, Jiménez-Reyes P. Load-velocity profiling in the military press exercise: Effects of gender and training. Int J Sports Sci Coach 2018;13(5):743-50. doi: 10.1177/1747954117738243 [Crossref]
- Conceição F, Fernandes J, Lewis M, Gonzaléz-Badillo JJ, Jimenéz-Reyes P. Movement velocity as a measure of exercise intensity in three lower limb exercises. J Sports Sci 2016;34(12):1099-106. doi: 10.1080/02640414.2015.1090010 [Crossref]
- Jidovtseff B, Harris NK, Crielaard J-M, Cronin JB. Using the load-velocity relationship for 1RM prediction: J Strength Cond Res 2011;25(1):267-70. doi: 10.1519/JSC.0b013e3181b62c5f [Crossref]
- Martínez-Cava A, Morán-Navarro R, Sánchez-Medina L, González-Badillo JJ, Pallarés JG. Velocity- and power-load relationships in the half, parallel and full back squat. J Sports Sci. 2019 May 19;37(10):1088-96. doi: 10.1080/02640414.2018.1544187 [Crossref]
- Sánchez-Medina L, González-Badillo J, Pérez C, Pallarés J. Velocity- and power-load relationships of the
bench pull vs. bench press exercises. Int J Sports Med 2013;30;35(03):209-16.
- González-Badillo J, Marques M, Sánchez-Medina L. The importance of movement velocity as a measure to control resistance training intensity. J Hum Kinet 2011;29A(Special-Issue):15-9. doi: 10.2478/v10078-011-0053-6 [Crossref]
- McBurnie AJ, Allen KP, Garry M, Martin M, Thomas D, Jones PA, et al. The benefits and limitations of predicting one repetition maximum using the load-velocity relationship. Strength Cond J 2019;41(6): 28-40. doi: 10.1519/SSC.0000000000000496 [Crossref]
- García-Ramos A, Suzovic D, Pérez-Castilla A. The load-velocity profiles of three upper-body pushing exercises in men and women. Sports Biomech 2019;1-13. doi: 10.1080/14763141.2019.1597155 [Crossref]
- Muñoz-López M, Marchante D, Cano-Ruiz MA, Chicharro JL, Balsalobre-Fernández C. Load-, force-, and power-velocity relationships in the prone pull-up exercise. Int J Sports Physiol Perform 2017;12(9):1249-55. doi: 10.1123/ijspp.2016-0657 [Crossref]
- Sale DG. Neural adaptation to resistance training. Med
Sci Sports Exerc 1988;20(Sup 1):S135-45.
- Kraemer WJ, Ratamess NA. Fundamentals of resistance training: progression and exercise prescription. Med Sci Sports Exerc 2004;36(4):674-88. doi: 10.1249/01.mss.0000121945.36635.61 [Crossref]
- Torrejón A, Balsalobre-Fernández C, Haff GG, García-Ramos A. The load-velocity profile differs more between men and women than between individuals with different strength levels. Sports Biomech 2019;18(3):245-55. doi: 10.1080/14763141.2018.1433872 [Crossref]
- Pallarés JG,
Cava AM, Courel-Ibáñez J, González-Badillo JJ, Morán-Navarro R. Full squat produces greater neuromuscular
and functional adaptations and lower pain than partial squats after prolonged
resistance training. Eur J Sport Sci 2019;1-10. doi: 10.1080/17461391.2019.1612952 [Crossref]
- García-Ramos A, Haff GG, Pestaña-Melero
FL, Pérez-Castilla A, Rojas FJ, Balsalobre-Fernández
C, et al. Feasibility of the 2-point method for determining the 1-repetition
maximum in the bench press exercise. Int J Sports Physiol
Perform 2018;13(4):474-81. doi: 10.1123/ijspp.2017-0374 [Crossref]
- Pérez-Castilla A, Jaric S, Feriche B, Padial P, García-Ramos A. Evaluation of muscle mechanical capacities through the two-load method: optimization of the load selection. J Strength Cond Res 2018;32(5):1245-53. doi: 10.1519/JSC.0000000000001969 [Crossref]
- Hartmann H, Wirth K, Klusemann M. Analysis of the load on the knee joint and vertebral column with changes in squatting depth and weight load. Sports Med 2013;43(10):993-1008. doi: 10.1007/s40279-013-0073-6 [Crossref]
- Pallarés JG,
Sánchez-Medina L, Pérez CE, De La Cruz-Sánchez E, Mora-Rodriguez R. Imposing a
pause between the eccentric and concentric phases increases the reliability of isoinertial strength assessments. J Sports Sci
2014;32(12):1165-75.
- Pareja-Blanco F, Rodríguez-Rosell D, Sánchez-Medina L, Gorostiaga E, González-Badillo J. Effect of movement velocity during resistance training on neuromuscular performance. Int J Sports Med 2014;35(11):916-24. doi: 10.1055/s-0033-1363985 [Crossref]
- Sánchez-Medina L, Pallarés J, Pérez C, Morán-Navarro R, González-Badillo J. Estimation of relative load from bar velocity in the full back squat exercise. Sports Med Int Open 2017;1(02):E80-8. doi: 10.1055/s-0043-102933 [Crossref]
- Heath BH, Carter JE. A modified somatotype method. Am J Phys Anthropol 1967;27(1):57-74. doi: 10.1002/ajpa.1330270108 [Crossref]
- Courel-Ibáñez J, Martínez-Cava A, Morán-Navarro R, Escribano-Peñas P, Chavarren-Cabrero J, González-Badillo JJ, et al. Reproducibility and repeatability of five different technologies for bar velocity measurement in resistance training. Ann Biomed Eng 2019;47(7):1523-38. doi: 10.1007/s10439-019-02265-6 [Crossref]
- Pérez-Castilla A, Piepoli A, Delgado-García G, Garrido-Blanca G, García-Ramos A. Reliability and concurrent validity of seven commercially available devices for the assessment of movement velocity at different intensities during the bench press. J Strength Cond Res 2019;33(5):1258-65. doi: 10.1519/JSC.0000000000003118 [Crossref]
- Hopkins WG, Marshall SW, Batterham AM, Hanin J. Progressive statistics for studies in sports medicine and exercise science. Med Sci Sports Exerc 2009;41(1):3-13. doi: 10.1249/MSS.0b013e31818cb278 [Crossref]
- Spitz RW, Gonzalez AM, Ghigiarelli JJ, Sell KM, Mangine GT. Load-velocity relationships of the back vs. front squat exercises in resistance-trained men. J Strength Cond Res 2019;33(2):301-6. doi: 10.1519/JSC.0000000000002962 [Crossref]
- Adams GR, Harris RT, Woodard D, Dudley GA. Mapping of electrical muscle stimulation using MRI. J Appl Physiol 1993;74(2):532-7. doi: 10.1152/jappl.1993.74.2.532 [Crossref]
- Haff G, Triplett NT, eds. National Strength &
Conditioning Association (US). Essentials of strength training and
conditioning. 4 ed. Champaign, IL: Human Kinetics; 2016. 735 p.